| The JAVA Applet |
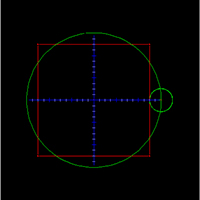
To change the shape of the picture, click in any red dot point and, with the left mouse button pressed, drag it to a new position!
To scale the picture, press the key “s” and, with it pressed, drag the mouse! To translate the picture, press the key “t” and, with it pressed, drag the mouse!
To reset the picture to its default position and size, press the key “r”. You may also reload this page to restart this applet!
You may also build your own examples! You just have to modify the applet JAVA parameters in this HTML file. The source code is here: fft.zip.
| Note |
During the first centuries of our era, the Ptolemaic school of astronomy studied extensively the possibility of describing a planetary orbit as follows. Start with a circle (the ideal figure) centered at some origin (typically, the Earth) and consider a celestial body turning around this circle at a fixed angular velocity. In complex notation, something that would be utterly misterious to ancient scientists, the orbit position would be given by
p(t) = r exp(i ω t). Now, this simply does not work: there were already measurements indicating that something better should be done. Their suggestion was very elegant: why not think that a second constant circular motion superimposes on this one, or, more generally, why not consider circles over circles over circles, which, in more precise terms, would give rise to orbits of the form
p(t) = r1 exp(i ω1 t) + r2 exp(i ω2 t) + r3 exp(i ω3 t) + … + rk exp(i ωk t), in the case of k circles.
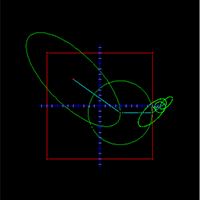
This turned out to be too good, in a sense. Not only this suffices to describe very well long stretches of planetary orbits, once the many parameters are well chosen, but one may, for example, take any continuous closed parametrized curve as a possible orbit with a good approximation by such sums. Notice that the angular velocities are not multiples of a common one: our ancestors would be able to describe orbits — at least along stretches — which were not necessarily closed.
In the applet above, we show how to draw a satisfactory Batman sign as a planetary orbit by choosing 64 circular motions, one on top of another. We were lazy with our choice of parameters. First, we supposed that all frequencies were integer multiples of a basic one. We also assembled terms of the formrk exp(i ωk t) with their almost twins r-k exp(i ω-k t): pairs like that give rise to ellipses instead of circles, as you will have not trouble showing, grouping real and imaginary parts appropriately. Also, some of the 32 ellipses are rather small, and in principle they might have been deleted from our description of the orbit.
The basic reason we decided to be so lazy was to show what is going on. Start with 64 points in the plane, chosen along a curve which draws a fair Batman sign, and now, think that the curve is being replaced by a piecewise linear function f obtained by interpolation from the 64 equally spaced points in the interval [0, 2 π]. Now, the frequenciesωk are simply (positive and negative) multiples of π and the
rk's are, up to normalization, the coefficients of the Fourier series of f, balanced around 0. This is what the Fast Fourier Transform does for you.
| Others Examples |


| Acknowledgments |
This applet was developed using the graphical library JAVAVIEW.
The Complex Number and FFT classes were taken from a Princeton's Computer Science Course.
The array initialization using HTML parameters was provided by Yvon Sauvageau.
A very good and concise background of the theory is given here: Discrete Fourier Transform (Wikipedia).
